많이들 들어보았을 것이다. 인간은 10진법, 컴퓨터는 2진법.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9. 인간이 10진법을 쓰는 방법으로 숫자를 표기해 사용한다.
그렇다면 컴퓨터는 어떻게 2진법을 사용하는 것일까.
컴퓨터의 내부에는 수많은 트랜지스터가 존재하는데, 이 트랜지스터를 전기 신호를 통해
켰다 껐다 할 수 있다. 여기 트랜지스터가 켜지면 on(true), 꺼지면 off(false) 상태라고 볼 수 있다.
컴퓨터는 이 상태를 각각 1, 0으로 인식하고 이를 통해 2진법을 사용할 수 있는 것이다.
뭐 이런 건 차치하고, 왜 10진수가 아닌 다른 것들도 배워야 할까?
그 이유는 나중에 배울 비트 연산을 위해서이다. 비트 연산자를 통해 추후 비트 마스킹과 같은
기법들을 활용할 때가 오는데, 그 때를 위해 공부해 두어야 한다.
우선 10진수를 다른 진수로 변환하는 방법을 알아보자.
70이라는 숫자를 2진수로 표현하려면
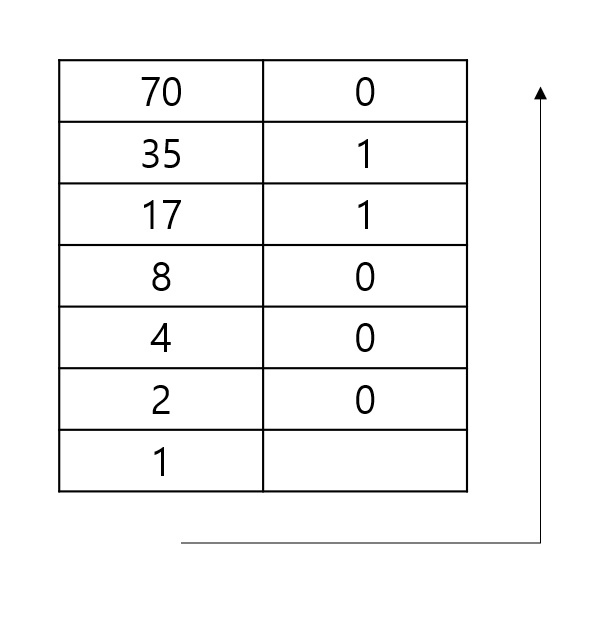
70을 2로 나누면 나머지가 0이다.
나눈 35를 또 나누면 나머지가 1이다.
이런 식으로 쭉 내려가다보면 1이 되는데
이때 거꾸로 읽어나가는 것이다.
즉, 70의 2진수는 1000110이 되는 것이다.
마찬가지로 70을 8진수로 표현하면
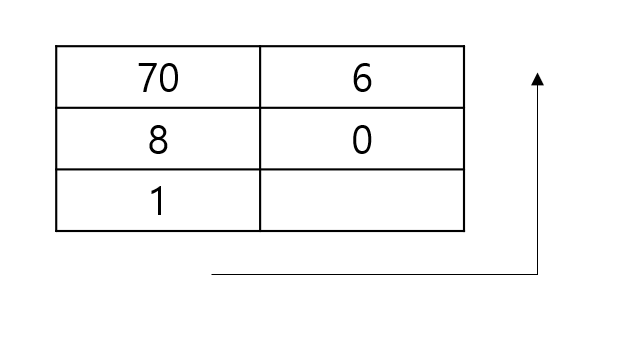
70의 8진수는 106이다.
마지막으로 70을 16진수로 표현하면

46이 된다.
반대의 경우에는 각 자리수마다 진수의 자리수 제곱을 곱해주면 되고,
각 진수간 변환은 2진수에서 8진수는 3자리씩 묶어서 계산하고,
2진수에서 16진수는 4자씩 묶어서 계산하면 된다.
이를 통해 다양한 진수를 표현하고 또 계산할 수 있다.
위에서 말했듯이 컴퓨터는 2진수를 사용한다고 했는데,
컴퓨터가 2진수를 사용하는 방법에 대해 알아보자.
우선 컴퓨터에서는 음수 또한 2진수를 활용한다.
최상위 비트를 부호 비트로 활용해서 양수일 때는 0, 음수일 때는 1로 표시한다.
예를 들어 4와 -4인 경우

이렇게 표시할 수 있다.
이는 가장 직관적이면서 쉬운 방법이기도 하다.
하지만 이 방법은 단점이 크다. 양수와 양수, 음수와 음수의 덧셈을 표현하는 것에는 큰 문제가 없지만
음수와 양수의 합의 경우에는 고려해야할 것이 많아지기 시작한다. 단순하게 더해버리면 제대로 된 값이
나오지 않기도 하고, 부호를 표시하는 비트와 숫자를 표시하는 비트를 따로 계산해주기도 해야 해서
머리가 아프다.
라고 이해했다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 비트마스크(BitMask) - 비트 연산 (0) | 2023.03.22 |
|---|---|
| 분할 정복 (0) | 2023.03.22 |
| 1의 보수(One's Complement) (0) | 2023.03.22 |
| 시간 복잡도 (0) | 2023.03.21 |
| 복잡도 (0) | 2023.03.21 |
