KMP 알고리즘은 패턴 매칭에 사용되는 알고리즘으로
Knuth, Morris, Pratt이라는 천재 세명이 만든 알고리즘이다.
기본적인 개념은 패턴을 매칭하는 과정에서 불일치가 발생한 텍스트 문자열의 앞 부분에
어떤 문자가 있는지를 미리 알고, 이를 통해 불일치가 발생한 앞 부분에 대해 다시 비교하지 않고 매칭을 수행할 수 있다.
라는 개념이다.
브루트 포스로다가 때려 박아서 비교하는 거는 시간 복잡도가 O(MN)이되는데 반해,
KMP 알고리즘의 시간 복잡도는 O(N+M)이 된다. 여기서 N은 문자열 길이이고, M은 패턴의 길이다.
이런 개념을 가지고 KMP 알고리즘을 알아보자.
일단 KMP알고리즘은 접두사와 접미사를 차례대로 이용한다.
ABCABCABC 라는 문자가 있다면
한개를 비교할 때의 접두사와 접미사는
A와 C이다.
그렇다면 두개는?
AB와 BC다
이걸 표로 만들어보면 다음과 같다.

즉 끝에서 몇개까지 읽냐에 따라 접두사와 접미사는 위와 같이 변한다.
그럼 이를 어떻게 이용하냐
읽는 개수를 i라고 할때, 0에서i까지의 문자열 중에 접두사와 접미사가 같은 경우의 길이를 구하는 것이다.

이렇게 접두사 부분과 접미사 부분을 비교해 길이를 구하고, 이 길이를 활용한다.
KMP의 알고리즘에서는 패턴을 통해 얼마나 이동할 지를 결정할 배열이 필요하다.
여기서 위에서 구한 길이가 필요하다.
우선 코드로 보자면
static int [] getTable(String pattern){
int [] arr= new int [pattern.length()]; //이동 위치 저장 배열
char [] pt = pattern.toCharArray();
int j=0; //패턴 문자열을 순회하면서 비교할 인덱스
for(int i=1;i<pattern.length();i++){ // 패턴 문자열을 진행하면서 비교할 인덱스 i
while(j>0 &&pt[i]!=pt[j]){ //j가 0이 아닐 때, 즉 i자리와 0번째 자리가 같아서 비교하고 있을때,
//근데 i번째랑 j번째 문자가 다를때,
j=arr[j-1]; //이동 위치 저장한 배열에서 저장된 위치로 거듭해서 올라감
}
if(pt[i]==pt[j]){//만약 같다면
arr[i]=++j;//이동위치 저장 배열에 j를 1더한 뒤 저장
}
return arr; //이동 위치 저장 배열 반환
}코드로 보면 복잡하지만 어느 정도 이해가 가능할 것이다.
j는 반복해서 패턴을 비교해주는 문자고 i는 패턴에서 쭉 나아가면서 비교해주는 인덱스다
ABCDABA 패턴 문자열을 예로 들면

이런 상태에서 시작한다.
j는 0이고, A와 B는 다르기 때문에 i++

또한 j는 0이고, A와 C는 다르기 때문에 i++
i가 가리키는 게 D일 때도 마찬가지이기 때문에 넘어간다.
그럼 i와 j 가 가리키는 게 둘 다 A일때는 어떨까?
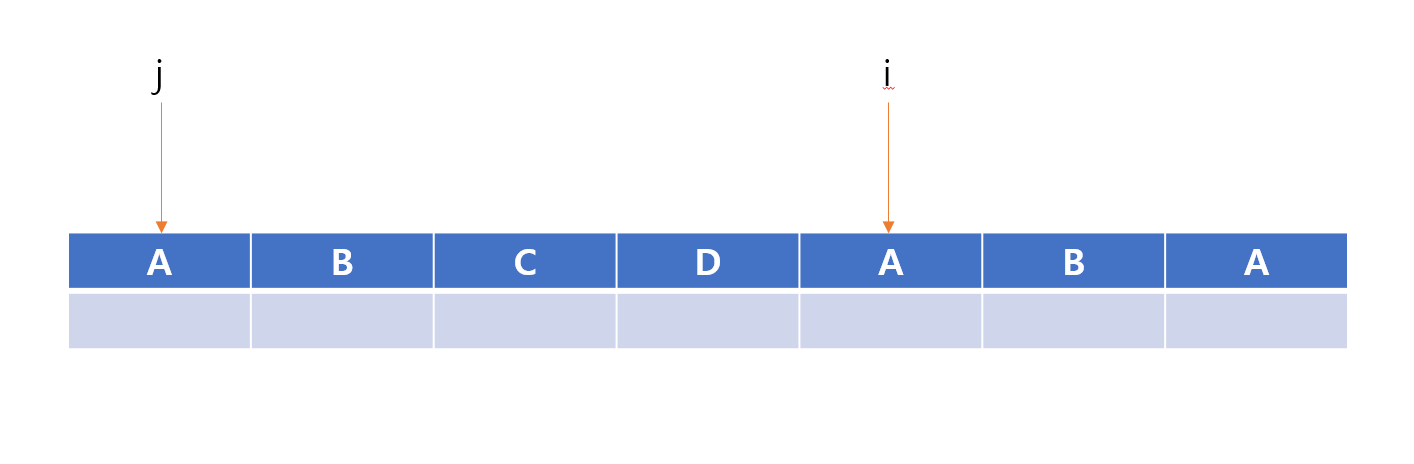
이 상태다.
그렇다면 위의 코드와 같이 arr[i]=++j 를 해주어야 한다.
그럼 그전에 있던 문자들의 위치에서의 arr 값은?
자바에서는 배열 초기값이 0이기 때문에 그대로 0이다.
이를 작성해보면 다음과 같다.
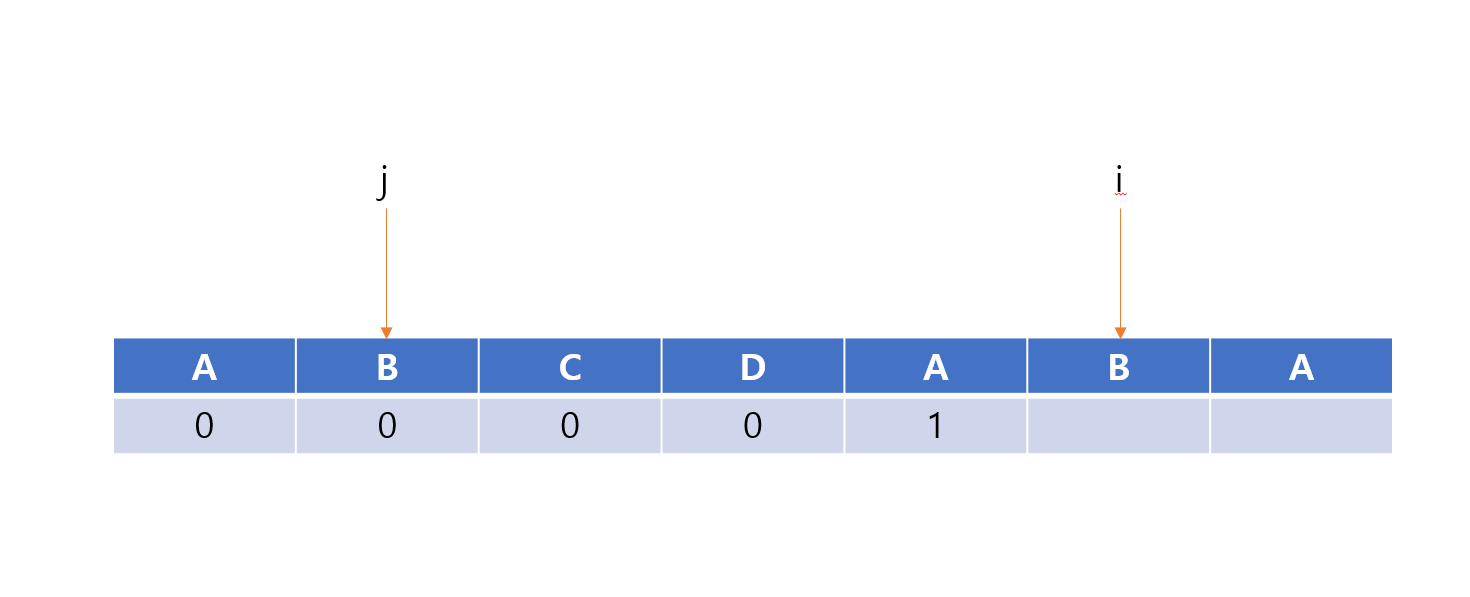
이 경우에도 같으니 똑같이 arr[i]=++j를 해주자.
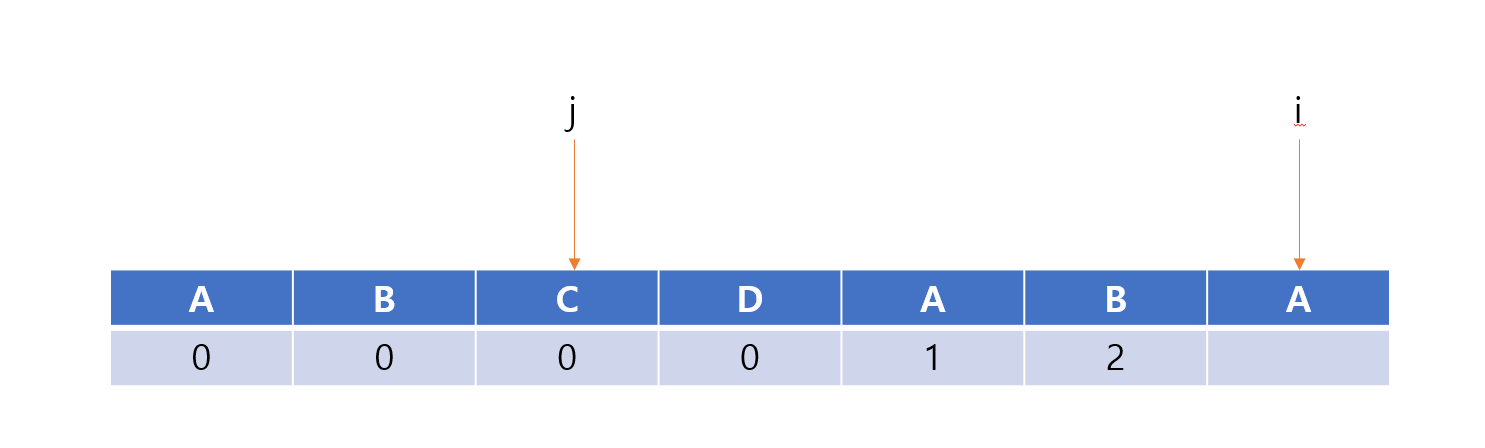
이렇게 작성할 수 있다.
하지만 이제는 i와 j가 가리키는 것이 다르고, j가 0이상이기 때문에 while문 안에 있는 코드들을 실행할 때가 왔다.
j=arr[j-1] 을 해준다. 즉, 처음에는 직전의 배열에 들어있는 값을 할당해준다.
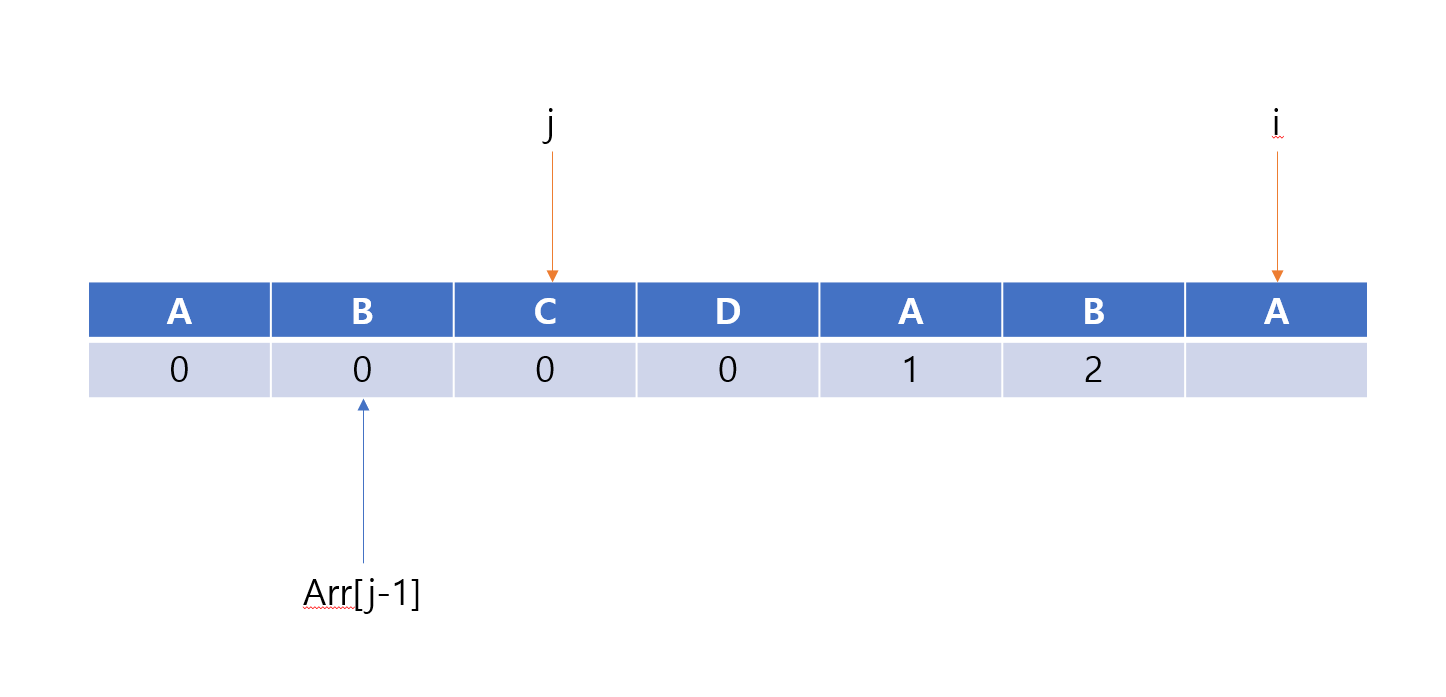
즉, j에는 arr[j-1]에 들어있는 0의 값이 할당되는 것이다.
그럼 다시 while문으로 돌아가서 j>0이 아니기 때문에 탈출하게 되고,
A와 A는 같기에 ++j를 넣어주고 끝난다.
최종 배열은 다음과 같다.
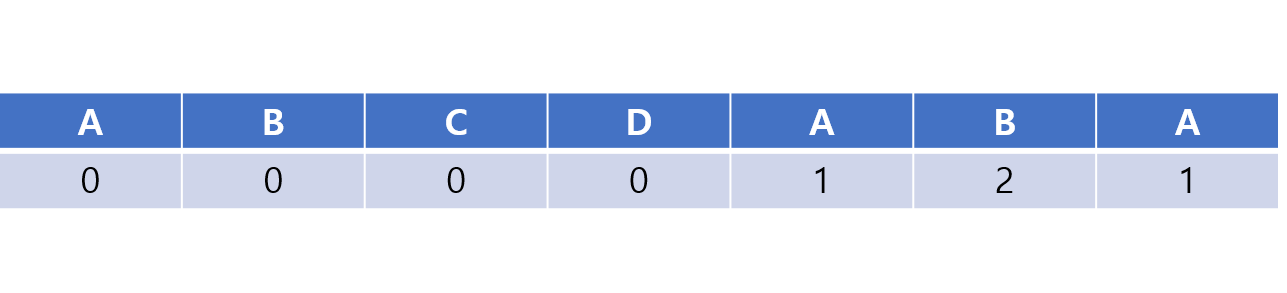
이것을 이용해서 전체 문자열과 패턴을 비교하게 되는 것이다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| Rabin-Karp 알고리즘 (0) | 2023.04.14 |
|---|---|
| KMP 알고리즘(2) (0) | 2023.04.14 |
| 위상정렬 (0) | 2023.04.03 |
| Dijkstra 알고리즘 (0) | 2023.03.30 |
| Prim 알고리즘 (0) | 2023.03.30 |
