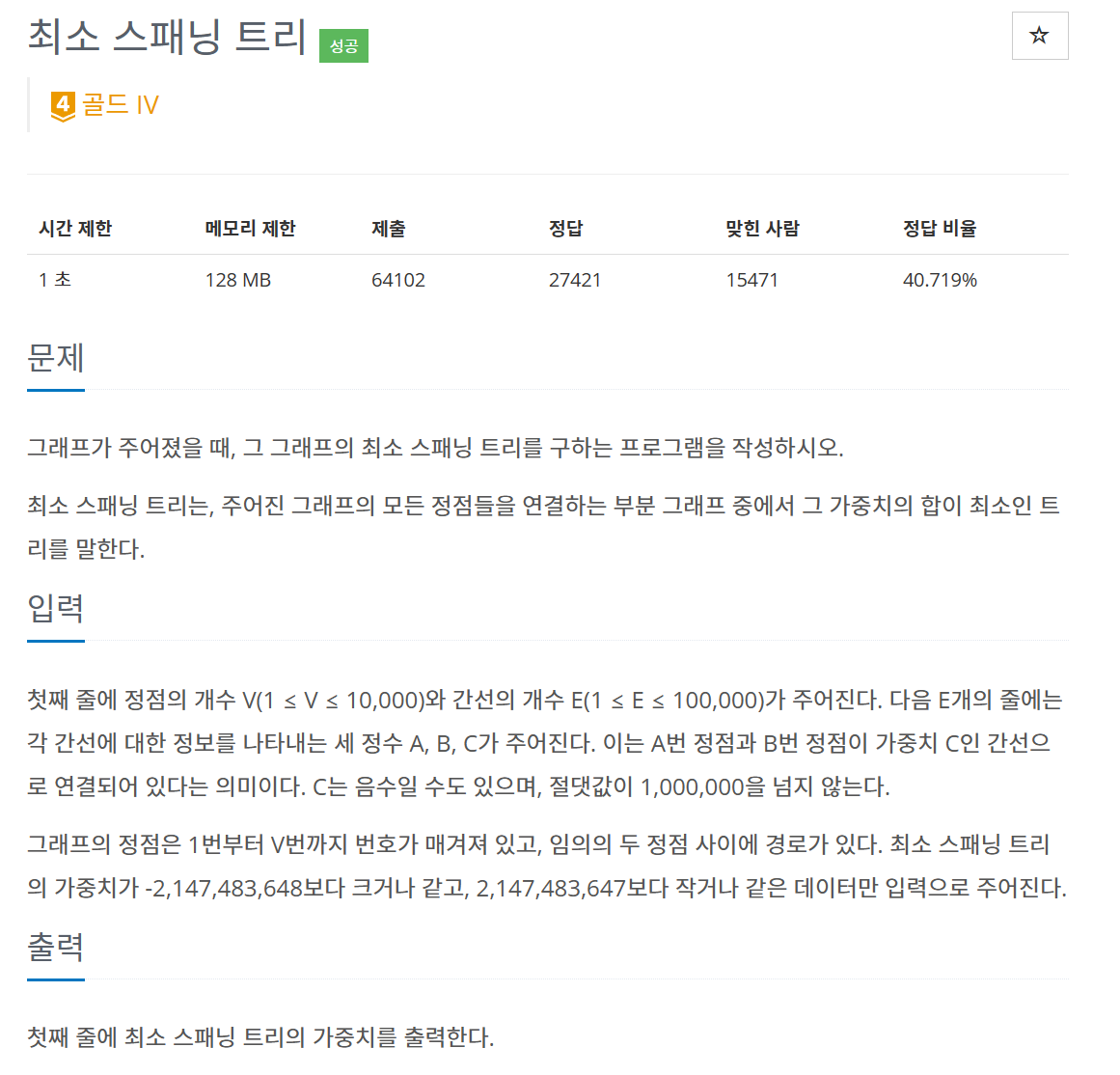
해당 문제의 조건은 위와 같다.
나는 이 문제를 크루스칼 알고리즘을 통해 풀었다.
우선 정점의 개수와 간선의 개수를 입력 받고,
간선의 개수만큼 배열을 만든다.
이때 배열은 2차원 배열로 A 정점, B 정점, 가중치를 입력받게끔 edges[i][3] 으로 만든다.
StringTokrenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int [][] edges = new int [e][3];
이런 식으로 만든 다음 차례대로 입력을 받는다.
for(int i=0;i<e;i++){
st = new StringTokenizer(br.readLine());
edges[i][0]=Integer.parseInt(st.nextToken());
edges[i][1]=Integer.parseInt(st.nextToken());
edges[i][2]=Integer.parseInt(st.nextToken());
}
받은 입력을 차례대로 저장한다.
이를 크루스칼 알고리즘의 첫번째 스텝인 오름차순 정렬한다.
Arrays.sort(edges, new Comparator<int[]>(){
@Override
public int compare(int [] o1,int []o2){
return o1[2]-o2[2]; //o1배열의 가중치가 작으면 그대로, 크면 바꿔주게끔
}
});
정렬이 되었다면
간선의 가중치를 합하기 위한 변수와
선택한 간선의 수를 저장할 변수를 만든다.
그 후 집합을 만든다. 초기화는 각각 자신이 자신의 대표 원소로 만들기(Make-Set)
static int p;//전역
p=new int[v+1];//접근하기 쉽게
for(int i=1;i<=v;i++){
p[i]=i;
}
각 정점이 자기 자신을 대표하는 서로소 집합이 되었다.
이를 이제 가중치를 비교해 정렬한 배열을 바탕으로 연결하자.
여기에서는 Find-Set, Union 연산이 필요하다.
for(int i=0;i<e;i++) {
if(findset(edges[i][0])!=findset(edges[i][1])){//만약 두 정점이 서로소 집합이라면
union(edges[i][0],edges[i][1]);//합집합으로 만들어 주고
result+=edges[i][2];//간선 가중치를 더한 뒤
cnt++;// 간선 선택 수 추가
}
}
private static void union(int i, int j) {// 한 집합의 루트 노드의 부모 노드를
// 다른 집합의 루트 노드로 만들어 준다.
// TODO Auto-generated method stub
p[findset(i)]=findset(j);
}
private static int findset(int i) { // 해당 노드를 쭉 타고 올라가 루트 노드 확인하기
// TODO Auto-generated method stub
if(p[i]==i)return i; //루트 노드면 루트 노드 반환
p[i]=findset(p[i]); //루트 노드가 아니면 부모를 루트 노드로 바꿈
return p[i]; //해당 노드의 부모노드 반환(결국 루트 노드 반환)
}
이렇게 findset 연산을 통해 서로소를 확인하고
서로소이면 합집합으로 만들고
가중치를 더하고
간선 수를 추가한다.
전체 코드는 다음과 같다.
package prac;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.Comparator;
import java.util.StringTokenizer;
public class Main {
static int[] p;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int [][]edges = new int [e][3];
for(int i=0;i<e;i++) {
st= new StringTokenizer(br.readLine());
edges[i][0]=Integer.parseInt(st.nextToken());
edges[i][1]=Integer.parseInt(st.nextToken());
edges[i][2]=Integer.parseInt(st.nextToken());
}
Arrays.sort(edges,new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
// TODO Auto-generated method stub
return o1[2]-o2[2];
}
});
int result=0;
int cnt=0;
p=new int [v+1];
for(int i=1;i<=v;i++) {
p[i]=i;
}
for(int i=0;i<e;i++) {
if(findset(edges[i][0])!=findset(edges[i][1])){
union(edges[i][0],edges[i][1]);
result+=edges[i][2];
cnt++;
}
}
bw.write(String.valueOf(result));
bw.close();
br.close();
}
private static void union(int i, int j) {
// TODO Auto-generated method stub
p[findset(i)]=findset(j);
}
private static int findset(int i) {
// TODO Auto-generated method stub
if(p[i]==i)return i;
p[i]=findset(p[i]);
return p[i];
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| 1504번 특정한 최단 경로 G4 (0) | 2023.04.03 |
|---|---|
| 1005번 ACM Craft G3 (0) | 2023.04.03 |
| 2252번 줄 세우기 G3 (0) | 2023.04.03 |
| 백준 1922번 네트워크 연결 G4 (0) | 2023.03.29 |



