지난 번에 서로소 집합, 즉 상호 배타 집합에 대해 알아 보았다.
이번에는 상호 배타 집합 연산에서 Rank를 이용한 방법과 Path Compression을 이용한 방법을 알아보자.
우선 Rank를 이용하는 것은 간단하다.
각 노드는 자신을 루트로 하는 SubTree의 높이를 Rank라는 이름으로 저장한다.
이를 이용해 두 집합을 합칠 때 Rank가 낮은 집합을 Rank가 높은 집합에 붙이는 것이다.

위와 같이 랭크가 2인 루트 노드에 랭크가 1인 루트 노드를 붙이면
랭크의 증가 없이 추가할 수 있다.
그렇다면 랭크가 같은 경우는 어떨까?

랭크가 같은 경우 일단 이어 붙인 후
랭크를 증가시켜줘야 한다.
다음은 랭크를 통한 Union 연산이다.
Union(x,y){
cal(Find-Set(x),Find-Set(y))
}
cal(x,y){
if(rank[x]>rank[y]){
parent[y]=x;
}
else{
parent[x]=y;
if(rank[x]==rank[y]){
rank[y]++;
}
}
}일단 각 집합의 대표 원소가 가지는 Rank값을 비교하고,
Rank가 높은 집합에 그렇지 않은 집합을 붙인다.
이때, 랭크가 같으면, 합집합의 대표 원소를 가지는 집합의 랭크를 ++ 해주는 것이다.
이런 식으로 랭크의 크기에 따라 연산을 실행하면 편향 트리 구조보다 나은 연산 능력을 기대할 수 있다.
그렇다면 Path Compression에 대해 알아보자.
Path Compression은 말그대로 경로 압축이다.
트리에서 해당 노드의 대표 노드를 확인하기 위해서는 Find-Set 연산을 통해
반복해서 거슬러 올라가 루트 노드를 찾는데,
이를 개선한 것이 Path Compression이다.
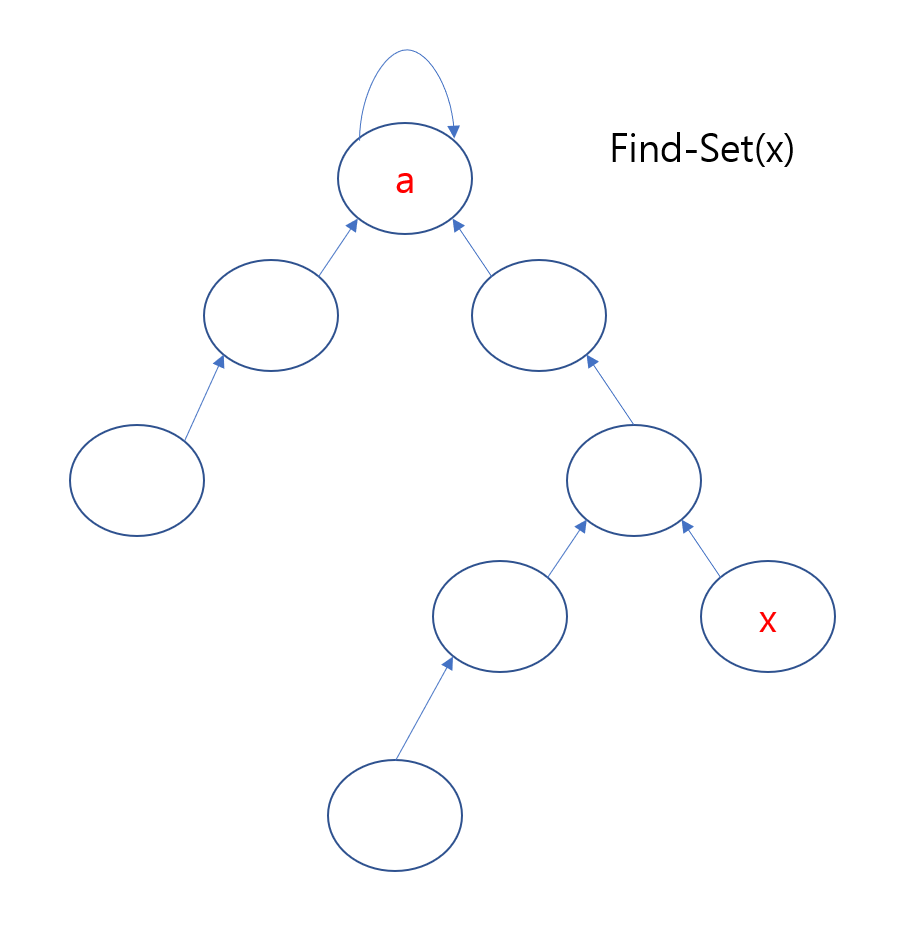
위와 같은 경우 Find-Set 연산을 실행하면 다음과 같아진다.
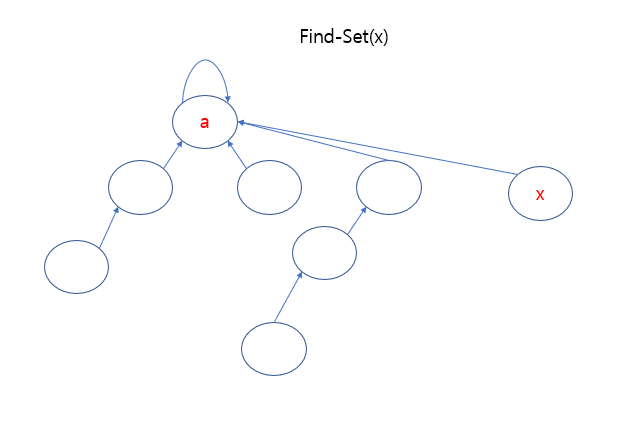
x 노드부터 거슬러 올라가면서 부모 노드를 대표 노드로 바꿔주는 것이다.
엄밀히 말하자면 루트 노드를 찾은 후, 다시 return 하면서 바꿔주는 것이다.
이를 코드로 표현하면 다음과 같다.
Find-Set(x){
if(x!=parent[x]){
parent[x]=Find-Set(parent[x]);
}
return parent[x];
}
만약 해당 노드가 루트 노드가 아닐 경우, 해당 노드의 부모 노드를 Find-Set(부모노드) 로 바꿔주는 것이다.
즉 재귀 호출을 통해 루트 노드로 올라갈 때까지 실행하고, 위에서부터 차례대로 부모노드를 루트노드로 바꿔주는 것이다.
이를 통해 해당 노드에서 바로바로 대표노드를 확인할 수 있는 것이다.
라고 이해했다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| Kruskal 알고리즘 (MST) (0) | 2023.03.29 |
|---|---|
| 최소 비용 신장 트리(Minimum Spanning Tree, MST) (0) | 2023.03.29 |
| 서로소 집합, 상호 배타 집합(Disjoint-Sets) (0) | 2023.03.29 |
| 백트래킹 (0) | 2023.03.24 |
| 비트 마스크(Bit Mask) - 활용(순열) (0) | 2023.03.24 |

